DIN 1045-1: Begrenzung der Rissbreite
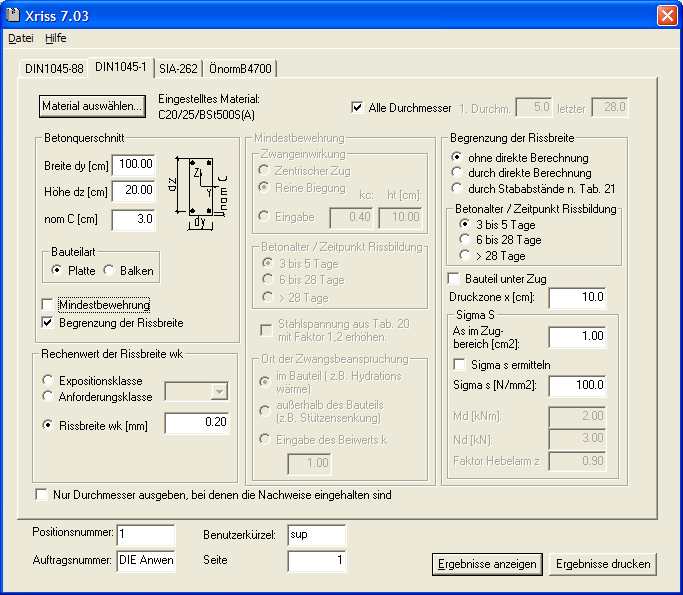
Hier stellen Sie ein, auf welche Art der Nachweis zur Begrenzung der Rissbreite geführt werden soll.
Ohne direkte Berechnung
Die Rissbreiten werden auf zulässige Werte begrenzt, wenn die Durchmesser der Bewehrungsstäbe in Abhängigkeit von der Spannung begrenzt werden DIN 1045-1 11.2.3.
Der Grenzdurchmesser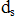 
* der Bewehrungsstäbe nach Tab. 20 wird in Abhängigkeit von der Bauteilhöhe und in Abhängigkeit von der wirksamen Betonzugfestigkeit 
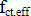folgendermaßen modifiziert:
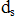* der Bewehrungsstäbe nach Tab. 20 wird in Abhängigkeit von der Bauteilhöhe und in Abhängigkeit von der wirksamen Betonzugfestigkeit 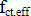folgendermaßen modifiziert:Gleichung 131 :
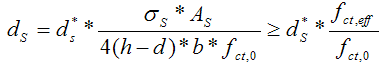
Die Berechnung von 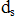* erfolgt nach Heft 525, 1.Auflage, Seite 196, Gl(21). Die Tab. 20 wurde durch Auswertung dieser Gleichung gewonnen.
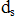* erfolgt nach Heft 525, 1.Auflage, Seite 196, Gl(21). Die Tab. 20 wurde durch Auswertung dieser Gleichung gewonnen.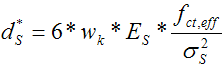
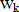 = | Rissbreite [mm] |
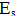 = | Elastizitätsmodul Stahl = 200000N/mm2 |
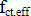| = | Wirksame Zugfestigkeit des Betons in N/mm2 zum betrachteten Zeitpunkt. |
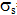 = | die Betonstahlspannung in N/mm2 im Zustand II für die maßgebende Einwirkungskombination |
Durch direkte Berechnung
Der Nachweis der Begrenzung der Rissbreite durch direkte Berechnung erfolgt nach DIN1045-1 Abschnitt 11.2.4.
Für den Rechenwert der Rissbreite 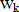gilt Gleichung 135:
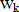gilt Gleichung 135: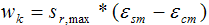
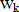| = | Rechenwert der Rissbreite [mm] |
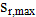 = | maximaler Rissabstand [mm] bei geschlossenem Rissbild |
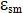 = | die mittlere Dehnung der Bewehrung unter der maßgebenden Einwirkungskombination unter Berücksichtigung der Mitwirkung des Betons auf Zug zwischen den Rissen. |
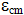 = | die mittlere Dehnung des Betons zwischen den Rissen |
Die Differenz der mittleren Dehnungen von Beton und Betonstahl wird wie folgt berechnet Gleichung 136:
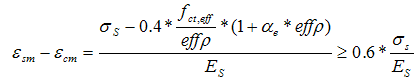
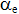 = | das Verhältnis der Elastizitätsmoduln Stahl / Beton =  | ||||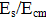
| effp = | der effektive Bewehrungsgrad nach DIN 1045 1 Gleichung 133  /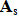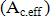 
| ||||
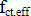| = | Wirksame Zugfestigkeit in N/mm2 des Betons zum betrachteten Zeitpunkt. | ||||
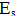| = | Elastizitätsmodul Stahl = 200000N/mm2 | ||||
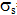| = | die Betonstahlspannung N/mm2 im Zustand II für die maßgebende Einwirkungskombination |
Der maximale Rissabstand 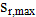wird nach DIN 1045 1 nach Gleichung 137 ermittelt:
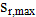wird nach DIN 1045 1 nach Gleichung 137 ermittelt: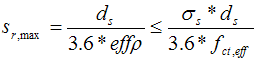
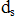| = | vorhandener Stabdurchmesser der Bewehrung | ||||
| effp = | der effektive Bewehrungsgrad nach DIN 1045 1 Gleichung 133 /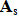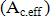
| ||||
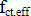| = | Wirksame Zugfestigkeit in N/mm2 des Betons zum betrachteten Zeitpunkt. | ||||
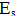| = | Elastizitätsmodul Stahl = 200000N/mm2 | ||||
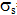| = | die Betonstahlspannung N/mm2 im Zustand II für die maßgebende Einwirkungskombination |
Durch Stababstände nach Tab 21.
Der Nachweis der Rissbreitenbegrenzung infolge überwiegender Lastbeanspruchung darf alternativ über eine Begrenzung der Stababstände geführt werden. Der Nachweis erfolgt mit Hilfe der Tabelle 21.
Die Berechnung des maximalen Abstandes erfolgt nach BK 2000 Abschnitt 3.2.4.3 Seite 228. Die Tab. 21 wurde durch Auswertung der Gleichung 3.79 gewonnen.
Gleichung 3.79
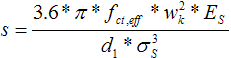
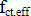| = | Rechenwert der Rissbreite [mm] |
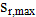| = | Wirksame Zugfestigkeit in N/mm2 des Betons zum betrachteten Zeitpunkt. |
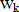| = | Rechenwert der Rissbreite [mm] |
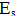| = | Elastizitätsmodul Stahl = 200000N/mm2 |
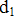 = | Randabstand der Zugbewehrung [mm] |
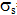| = | die Betonstahlspannung N/mm2 im Zustand II für die maßgebende Einwirkungskombination |
Die Ergebnisse nach Gleichung 3.79 sind sehr stark vom vorhandenen Randabstand der Zugbewehrung 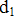abhängig. Für die Ermittlung der zulässigen Stababstände nach Tabelle 21 wurde 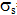= 4 cm angesetzt.
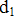abhängig. Für die Ermittlung der zulässigen Stababstände nach Tabelle 21 wurde 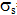= 4 cm angesetzt.Für Platten mit einlagiger Bewehrung ist diese Annahme ausreichend genau. Für Balken und bei mehrlagiger Bewehrung liegt diese Annahme auf der unsicheren Seite, so dass die zulässigen Stababstände zu groß ermittelt werden. Für diese Bauteile sollte der vereinfachte Nachweis der Rissbreitenbegrenzung deshalb über die zulässigen Stabdurchmesser geführt werden.
Betonalter /Zeitpunkt der Rissbildung
Hier stellen Sie ein, für welches Betonalter die wirksame Zugfestigkeit des Betons (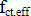) ermittelt werden soll. Hierzu siehe auch DIN 1045-1 Abschnitt 11.2.2.
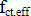) ermittelt werden soll. Hierzu siehe auch DIN 1045-1 Abschnitt 11.2.2.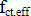= Wirksame Zugfestigkeit des Betons zum betrachteten Zeitpunkt.Bauteil unter Zug bzw. Druckzone x [cm]
Beim Nachweis durch direkte Berechnung ist die Angabe der Druckzonenhöhe x notwendig.
Hieraus ergibt sich 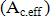der Wirkungsbereich der Bewehrung nach Bild 53.
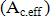der Wirkungsbereich der Bewehrung nach Bild 53.As im Zugbereich Lage [cm2]
Vorhandene Zugbewehrung für eine Querschnittsseite.
Sigma S ermitteln
Über diesen Schalter können Sie steuern, wie Sigma s (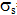),die vorhandenen Stahlspannung, ermittelt werden soll.
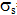),die vorhandenen Stahlspannung, ermittelt werden soll.Es stehen Ihnen 2 Möglichkeiten zur Verfügung:
- Schalter ist ausgestellt, die vorhandene Spannung kann im Eingabefeld Sigma s eingegeben werden.
- Schalter ist an, die vorhanden Spannung wird nach folgender Gleichung ermittelt:
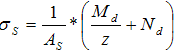
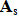| = | vorhandene Bewehrung |
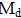 = | Bemessungsmoment [kNm] |
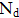 = | zugehörige Normalkraft [kN] |
| z= | Hebelarm aus der Betonbemessung Der Hebelarm wird aus dem Eingabewert „Faktor Hebelarm z“ und der Bauteilhöhe „ 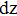 “ folgendermaßen ermittelt:z = Faktor * Bauteilhöhe |
sigma S [N/mm2]
Vorhandene Stahlspannung unter Annahme des Zustandes II aus der maßgebenden Einwirkungskombination.